
LeetCode Solutions工程師必學:遍歷二元樹使用中序(inorder)列印
在這篇文章中,說明二元樹這個資料結構的概念,它在計算機科學中非常重要,有很多演算法都一定會運用到這種資料結構,也是初入職場工程師必刷的leetcode考題。
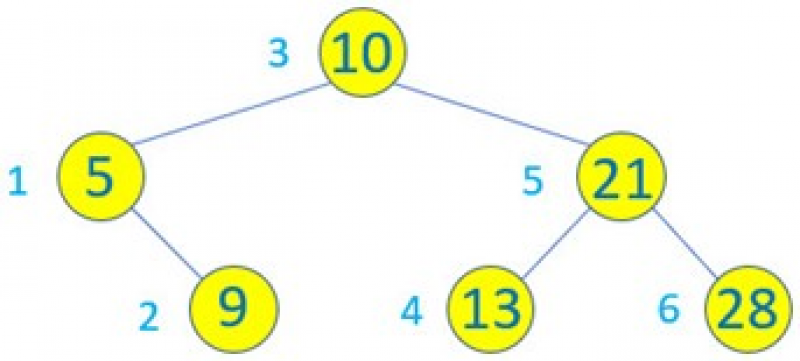
假設有一顆二元樹如下:
所謂中序列印是從左子樹往下走,直到無法前進就處理此節點,接著處理此節點的父節點,然後往右子樹走,如果右子樹無法前進則回到上一層。也可以用另一種解釋,遍歷左子樹(Left,縮寫是L)、根節點(Root,縮寫是D)、遍歷右子樹(Right,縮寫是R),整個遍歷過程簡稱是LDR。
用這個觀念遍歷上述二元樹可以得到下列結果:
5, 9, 10, 13, 21, 28
上述中序列印相當於可以得到由小到大的排序結果,如上所示,設計中序列印的遞迴函數步驟如下:
1:如果左子樹節點存在,則遞迴呼叫self.left.inorder( ),往左子樹走。
2:處理此節點(會執行此行,是因為左子樹已經不存在)。
3:如果右子樹節點存在,則遞迴呼叫self.right.inorder( ),往右子樹走。
程式實例ch6_4.py:使用10, 21, 5, 9, 13, 28系列數字建立一個二元樹,然後使用中序方式列印。

執行結果

下列二元樹節點左邊的數字是中序遍歷列出節點值的順序。
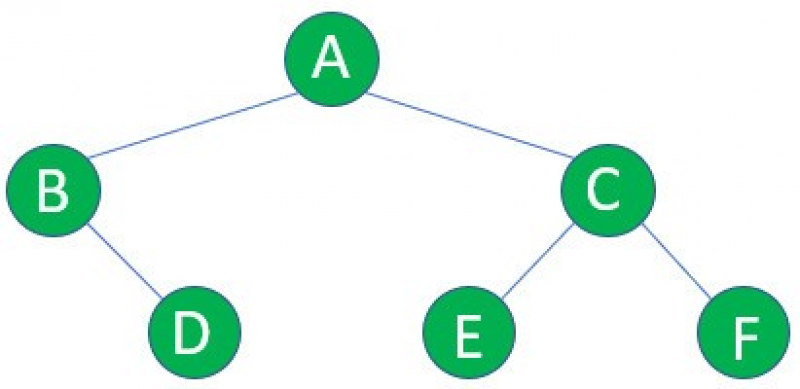
為了方便解說,將節點改為英文字母,然後使用二元樹和堆疊分析整個第25-31行遞迴inorder( )函數遍歷過程:
1:由A進入inorder( )。
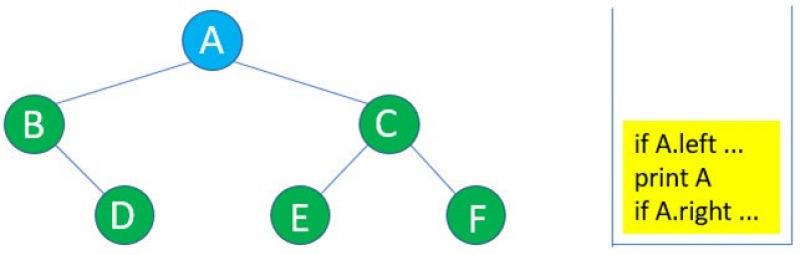
2:因為A的左子樹B存在,所以進入B的遞迴inorder( )。
3:B沒有左子樹,所以if B.left … 執行結束,圖形如下:
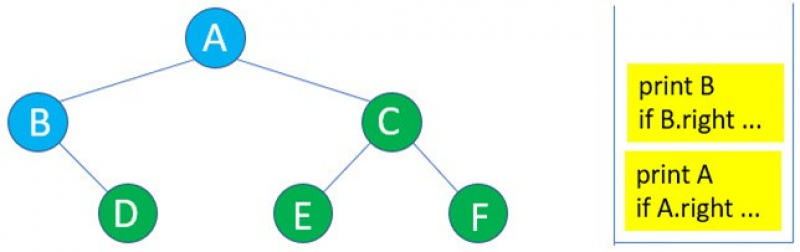
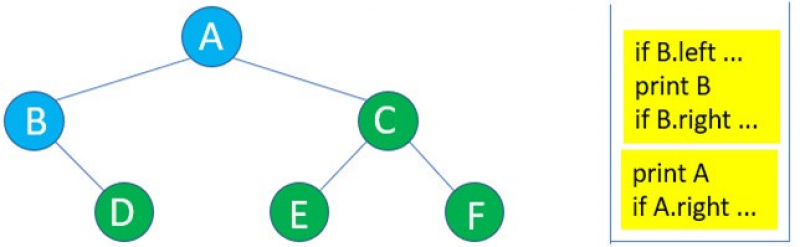
4:執行print B。
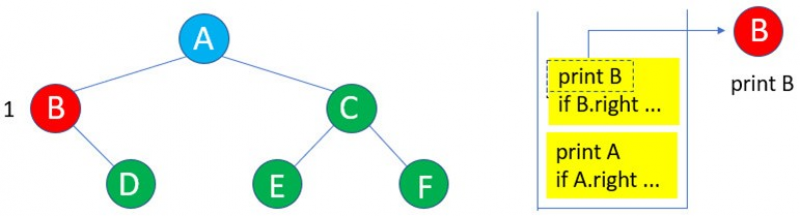
5:因為B的右子樹D存在,所以進入D的遞迴inorder( )。
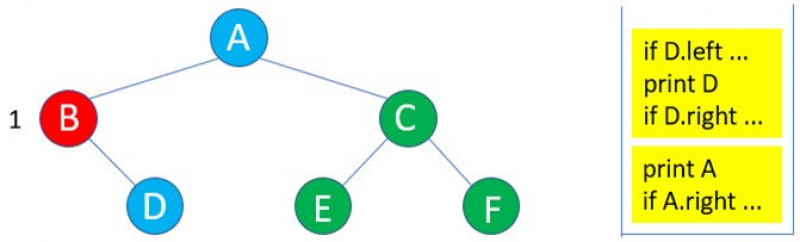
6:由於D沒有左子樹,所以if D.left … 執行結束,執行print D。
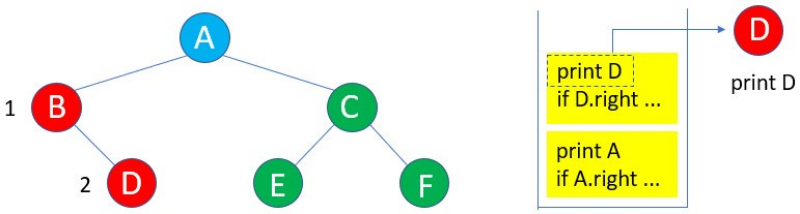
7:D沒有右子樹,所以if D.right … 執行結束,接下來執行print A。
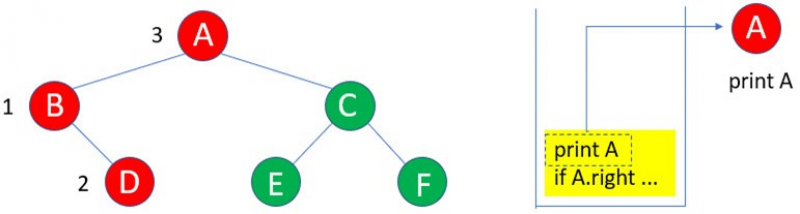
8:因為A的右子樹C存在,所以進入C的遞迴inorder( )。
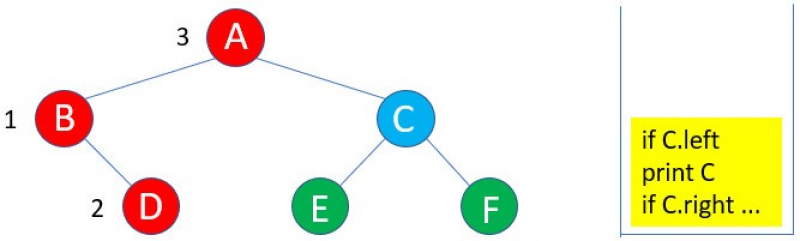
9:因為C的左子樹E存在,所以進入E的遞迴inorder( )。
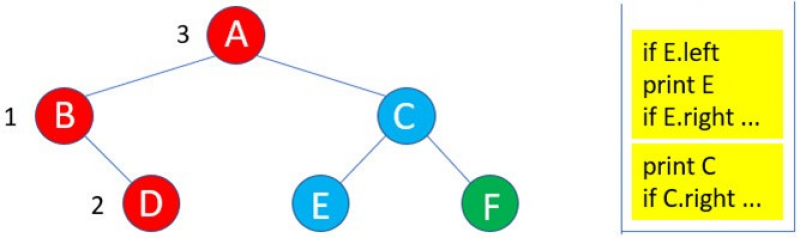
10:由於E沒有左子樹,所以if E.left … 執行結束,執行print E。
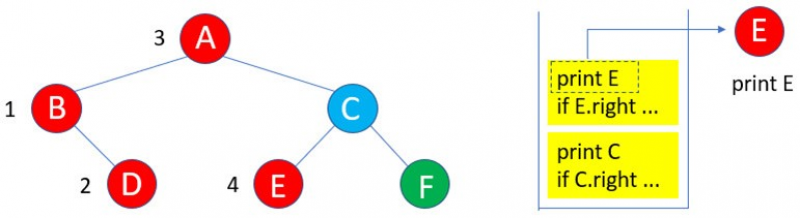
11:E沒有右子樹,所以if E.right … 執行結束,接下來執行print C。
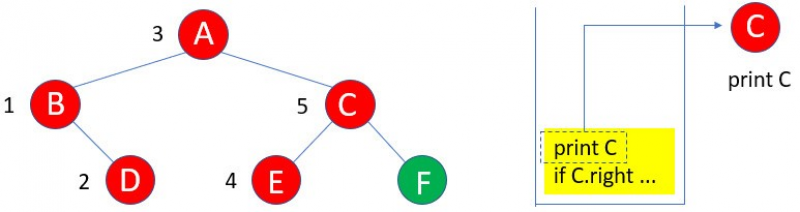
12:因為C的右子樹F存在,所以進入F的遞迴inorder( )。
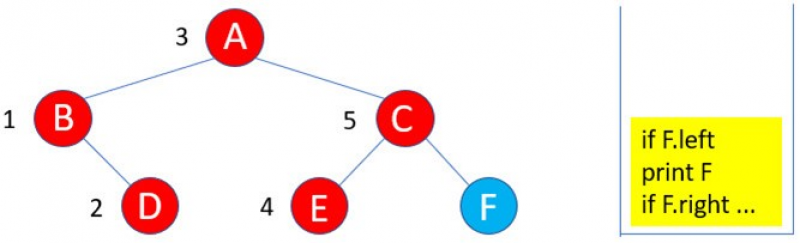
13:由於F沒有左子樹,所以if F.left … 執行結束,執行print F。
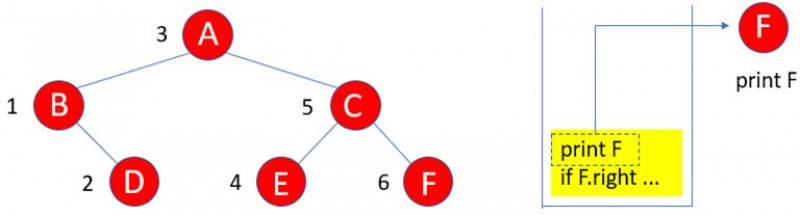
14:由於F沒有右子樹,所以執行結束。
上述節點旁的數值則是列印的順序。

執行結果

想閱讀更多請點我






















